大塚さん
大塚さん複利でお金が増えるのはわかったけど、計算がむずかしすぎるわ
 落合さん
落合さんおおよその計算なら暗算でできるよ
利子を元本に上乗せしていく複利は、お金を増やすのに効果的です。ただ、計算が複雑すぎるため何年後にどれくらいに増えるか直感的にわかりませんよね?
とっても簡単な式で、正確ではないですがほぼ近い値が暗算で計算できるようになるので説明しますね。
72の法則:リターンがわかれば何年後に2倍になるかは計算できる!
 大塚さん
大塚さん72の法則?72個も覚えられないわよ
 落合さん
落合さん法則は1個だよ。72になる数字を探す法則なんだ
72の法則とはリターン×年数が72になると資産が2倍になるという法則です。たとえばリターンが1%の場合、72年後に資産は2倍になります。
 大塚さん
大塚さんそんなわけないじゃない
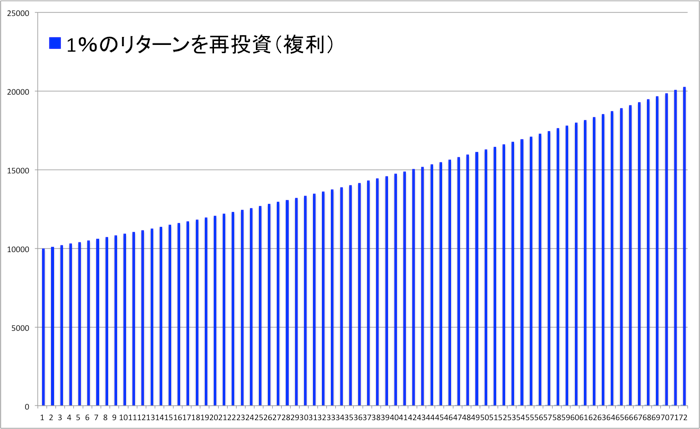
実際に10000円を年利1%の複利で72年あずけた場合のグラフになります。1年目に10000円だったお金は72年後に20470円になっています。
 大塚さん
大塚さん本当にほぼ2倍になってるわ
各利率で10,000円を預けるとどうなるか見てみましょう。
| 利率 | 年数 | 受取額 |
|---|---|---|
| 1% | 72年後 | 20,470円 |
| 2% | 36年後 | 20,399円 |
| 3% | 24年後 | 20,328円 |
| 4% | 18年後 | 20,258円 |
| 6% | 12年後 | 20,122円 |
| 8% | 9年後 | 19,990円 |
| 9% | 8年後 | 19,926円 |
| 12% | 6年後 | 19,738円 |
| 18% | 4年後 | 19,388円 |
| 24% | 3年後 | 19,066円 |
| 36% | 2年後 | 18,496円 |
| 72% | 1年後 | 17,200円 |
72となる利率と年数の組み合わせ表になります。8%が一番近く、そこから離れるにつれて精度は落ちますが、ほぼほぼ2倍になっていますよね。
 大塚さん
大塚さんこれは便利ね!
 落合さん
落合さんおおよその数字を暗算したいときに使えるよ
115の法則:リターンから3倍になるまでの年数がわかる
資産が3倍になるまでの年数は115の法則をつかって計算することができます。計算の仕方は72の法則と同じでリターン×年数が115になると資産が3倍になります。
 落合さん
落合さん115の法則もおおよその計算につかえるよ
各利率で10,000円を預けるとどうなるか見てみましょう。
| 利率 | 年数 | 受取額 |
|---|---|---|
| 1% | 115年後 | 31,402円 |
| 5% | 23年後 | 30,715円 |
| 23% | 5年後 | 28,153円 |
| 115% | 1年後 | 21,500円 |
 大塚さん
大塚さん115だと組み合わせが少なすぎて使いづらいわ
 落合さん
落合さんおおよその計算用だから、だいたい近い値になればいいよ
115となる利率と年数の組み合わせですと、4パターンしかないですね(汗)。
個人的な使い方ですが、暗算で3倍の複利計算がしたくなったら115に近くて組み合わせ数字が多い120で計算しています。
正確な値が知りたくなったらExcelなどで計算しますし、暗算でやるざっくり計算なら120でも桁がズレるほど外れないのでいいかなー、と。
まとめ
複利で2倍、3倍になる年数を暗算するマメ知識を紹介しました。
「Excelなどでキチンと計算しなさい」と思うかもしれませんが、毎回キチンと計算するのはめんどくさいんですよね(笑)
これを知っているだけで大きく外さない計算が暗算でできるようになるので、ぜひ頭の片隅にでも置いといてください。